Pendulum-Like motion of an unidentified object (UO) filmed by Billy Meier, Maccabee, Bruce, Internet, February 2002
NOTE IMPORTANTE
Cet article n'est pas une publication officielle de la FIGU.
PENDULUM-LIKE MOTION OF AN UNIDENTIFIED OBJECT (UO) FILMED BY BILLY MEIER
by Bruce Maccabee
ABSTRACT
This is an analysis of one of the many sightings presented by contactee Billy Meier of Switzerland over 25 years ago. This was the first sighting in which he claimed to obtain a movie of the spaceship of Semjase, a humanoid from the star group known as the Pleiades. This movie (and other Meier claims, photos and movies) have been the subject of extreme debate since they were first publicized over 20 years ago. I have carefully studied this movie and concluded that the motion of the UO (Unidentified Object) is consistent with the motion of a pendulum which is being driven by moving its suspension point. I can't say that Meier never had a UFO experience. However I do not use Meier's testimony/photos/videos as evidence that Other Intelligences (OI) are present in our airspace.
[The analysis of the oscillation period presented here was first published in the International UFO Reporter (IUR) in the Jan/Feb 1989 issue, published by the Center for UFO Studies under the title, "Pendulum from the Pleiades." The original text has been edited and information that was not in the original text has been added for this web presentation. None of the illustrations or pictures shown below were in the IUR publication. This presentation assumes that the reader has at least a fundamental knowledge of Billy Meier's claims of alien contacts, photos and movies.)
In November, 1988, I reviewed a video copy of the 8 mm movie of contactee Billy Meier of Switzerland. This copy is part of a videotaped interview of Meier by Jun-ichi Yaoi of Japan. He and a Japanese video crew visited Meier's home in the fall of 1979. They interviewed Meier and videotaped his photos and his movie. Meier's movie is a collection of short, 8 mm film strips made during some his sightings. For convenience in viewing, Meier had all the film strips spliced together to make one longer movie. The video cameraman videotaped the movie screen and recorded Meier's comments as the movie was being shown. As I viewed this videotape of the film I noticed that the camera was always stationary as the UOs moved into and out of view. Mr. Meier did not pan the camera with the UOs to keep them centered, even though he certainly could have done so during most of the filmings. Mr. Meier actually appeared in the movie film during one sighting (one segment of the film), but for the rest of the filmed sightings he is not seen. I also observed that sometimes a UO would wobble or rock or tilt back and forth a small amount and sometimes seem to bounce up and down a small amount when it moved.
I was particular interested in the first segment of the movie in which the path of the Unidentified Object (UO) often followed an arc that is convex downward, as if maintaining a constant, or nearly constant, distance from a point above, i.e., as if swinging about a suspension point. The UO moves left and right or back and forth over a tree which appears to be between the camera and a distant farmhouse. Meier claimed that he got this film on March 18, 1975. For comparison purposes Mr. Yaoi filmed from the same location. Figure 1, below, is a frame from Yaoi's video showing the scene where Meier filmed the UO. Note that there is a farmhouse in the distance but there is no tree blocking the view of the farmhouse. This is to be compared with the scene in Meier's film that is shown in the following illustrations.

[The words at the bottom of the picture call attention to the time code at the lower right corner that was added to the video by Yaoi's video crew. It, of course, does not appear in the original Meier film. The numbers shown in this frame represent elapsed time in hours (06), minutes (17), seconds (56) and frame number (8). The time indicated by the time code is unrelated to when Meier shot the original film. The presence of the time code makes it easy to locate specific frames in the video. During each second the frame numbers run from 0 (first frame in each second) to 29 (30'th frame of each second) corresponding to the standard 30 frames/sec video frame rate. The time code makes it simple to determine the time duration of each left-right oscillation.] The first video frame showing Meier's movie is 06:17:57, frame 15.
[Note: the original film is in color. Since color is not important here the images have been reduced to grey scale (color removed) to make the images clearer and to reduce the "bandwidth" (file size) needed for this web presentation.]
The opening scene of this segment of Meier's movie shows the house as background, visible on either side of an apparently large pine tree that has a stationary UO hanging over it.

The tree was not found during the investigations of Meier's claims. According to Meier the tree was killed by the spacecraft and subsequently removed by the Pleiadeans. This is at least one potential explanation for why the tree does not appear in Yaoi's video from the same location several years later.
While the UO remained stationary Yaoi's cameraman zoomed in on the movie screen by a factor of two (as determined by the change in image sizes; he increased or decreased the zoom several times after this). He also recorded Meier's verbal comments.
As this particular segment of Meier's movie was being shown Meier made the following statements. First, referring to the scene with the tree and farm house, Meier said "And that's the place where I got the first movie picture." That is, this was Meier's first movie of the "spaceship." At the very beginning the movie shows the UO slightly above and beside the tree, motionless. Meier said, "There was a tree staying (he meant "standing") there, where it's hanging over, the ship." (I.e., the ship was stationary over the tree.) He went on, "And that tree was eliminated later by Semjase, too."("Too" is a reference to another tree elimination by Semjase, the tree that is "featured" in the series of 10 photos at Fuchsbuel). "That picture (he means movie) I got, I think, February or March, 1975, in the evening time about half past five."
At this point, about 06:18:20 frame 15, the UO begins to move slowly to the left. That means that the UO has been motionless since the beginning of the movie, i.e., about 23 seconds. (One notes that this would give Meier time to start the camera and then begin to "operate" a UO support mechanism.) The UO moves slowly upward and to the left following an arc and then at about 06:18:26 abruptly starts to move downward and to the right, again following an arc.
During this initial motion of the UO Meier continues with his description of the weather conditions when he obtained this movie. "It was snowing, raining, and dusty (?, word not clear). And in front, between the tree and my (movie? word not clear) camera was some people working, a farmer, an old man and a child." (Note: these people do not appear in the video). At this point in the film the UO is moving slowly in small circles, with some wobble, around and just above the treetop. Meier says, "And if you have good eyes you can see that the ship isn't in front of the tree, it is a little bit behind the tree." By this time, 06:18:56, the UO has completed about 6 cycles of motion (left-right and circular, with increasing amplitude) near and above the tree.
Observation: the sky appears featureless in the movie (video) and the scene seems reasonably clear, i.e., not obstructed by snow, rain or dust.
During the next 10 seconds or so the amplitude of the motion... dare I say, "swinging" ... increases so that its speed increases and once again the oscillatory track nearly crosses the width of the video frame. Several times a slight wobble of the UO itself is added to the swinging motion. At about this time (06:19:08) Meier says, "And this flying, doesn't (isn't?) the normal flying of these ships. That's for demonstration only. If they are fly on the normal way...". At this point the UO is moving back and forth over the tree. Meier interjects into his previous sentence (06:19:21), "You have seen there how was moving the tree, now." This comment refers to a slight motion or bending to the right of the top of the tree at about 06:19:18 frame 20, as the UO passes over traveling from left to right , although the UO itself did not appear to touch the tree.
Meier resumes his commentary, "If they fly on the normal way they have a good line (he means straight flight track?) without this foolish jumping (he means wobble?) and everything." During this comment, just after the word "normal" there occurs the first UO "jump" in the film and then after his comment was finished there is another UO jump.
The jumps just referred to are from frame 06:19:26 #22 to 06:19:26 #23 and also from frame 06:19:37 #15 to 06:19:37 #16. In the first case the UO is moving right to left and it jumps from a location just to the right of above the tree to a location where it is centered above the tree. In the second case it is moving left to right and it jumps from a point nearly centered above the tree to a point a bit to the right of the tree. In other words, the "jump gap" (the portion of the motion that is missing) is at almost exactly the same location of the swing in each case (just to the right of the tree). During each jump the UO image moves about 80% of the width of the UO.
This jump in UO position certainly was not a result of an error Yaoi's video, for which the sound track (which picks up the voices and the continuous mechanical sound of Meier's movie projector) is continuous. The jump in UO position occurs at the same time as a vertical jump in the whole picture. This vertical jump in the picture, up and then down, is typical for 8 mm home movies that have been imperfectly spliced together. (When two sections of the film are spliced together the sprocket holes along the edge of each piece of film must be matched perfectly. Overwise the film slips a small amount as the splice travels through the framing mechanism. This slippage appears as a vertical jump in the picture on the screen until the sprocket teeth again match the sprocket holes exactly.) Hence one concludes that Meier's film itself had been cut and spliced at the locations of these frames. By comparison with the normal, continuous frame-by-frame motion of the UO it appears that about 12 frames were cut out of the film at each of these locations. The cutting of the film is obvious when the film is run at normal speed because one sees a vertical jump in the picture.
After the last comment Yaoi asked Meier if he could show the film again. At 06:19:42 there are about 15 dark frames in the video and then the movie appears again. The camerman, who zoomed in on the movie screen by a factor of two at the very beginning of the movie, zoomed in even further as they ran, several times, the few seconds of film which shows the tree moving.
The UO featured in this sighting/ movie segment does not show all the fine details of structure that are apparent in his photographs. Perhaps this is because the image, at least as it appears in the videotape, is not in perfect focus (nor is the background image of the tree nor is the farmhouse). The poor focus might be a result of Meier's movie camera not being well focused (intentionally? to hide fine details such as a supporting string?) or, less likely, it might be that Yaoi's video camera was not perfectly focused on the movie screen. Fortunately the analysis to be presented does not rely on good focus.
The film shows that initially the UO was stationary over the tree at the center of the picture [see Figure 2]. Then it slowly moved to the left and upward in an arc [see Figure 3]. [Note: the images of the tree and house are larger in this figure than in Figure 1 because the camera was zoomed in, as mentioned above.]

The UO accelerated to the right and downward in an arc and passed, apparently, over the tree and then upwards in an arc as it continued to the right. This motion is illustrated in the series of frames below.
Looking at the time codes in Figures 4 and 7 one can see that it required about 2 seconds and 8 frames or 8/30 = 0.27 sec, or 2.27 sec for the UO to cross the field of view. IF this UO were swinging on the end of a string like a simple pendulum, this would be one half of the period of oscillation. The complete period would be about 4.54 sec.
[Note: in the previous publication in IUR this period was noted as 5.1 seconds. This was because I counted the time continuously from the beginning of motion, through first half period to the maximum swing to the right and then through the second half period up to the maximum swing to the left. However, during the second half of the period the swing was modified from its normal motion in some way that caused wobbling and a shortening of the swing. This modification made the time duration of the second half about 2.8 seconds, whereas the time duration of the first half of the swing was only about 2.27 sec. As pointed out below, if the UO were moving with a pendulum-like motion, then modifications to the natural, unforced swing tend to increase the period. It is my opinion that the motion from left to right had less force applied than the subsequent motion from right to left. Hence, in my opinion the true free- pendulum period was closer to twice the period of the first half cycle.]
The UO then reversed direction and again traveled downward over the tree. The amplitude of the subsequent left-right oscillatory motions then decreased to nearly zero over many seconds, after which the amplitude of motion increased again and remained large. Whereas the initial motion was simply from the left to the right and back again, some of the subsequent large amplitude motion of the UO made an elliptical path as viewed on the screen and the sizes of the images changed periodically as the UO image traveled around this elliptical path. It is likely that the motion at this time was actually in a circular path in a horizontal plane but the path appears in the film to be elliptical because of the oblique viewing direction (from below and off to one side). Several times the UO almost disappeared at the left of the field of view of the videotape. Then the amplitude reduced gradually back down to zero so that once again the UO was apparently over the tree.
There is a period of time of considerable motion when the UO image moves right-left- right, etc. in an arc while the size of the UO image remains about constant. Because the image size is constant during this time one may assume that the distance to the UO itself was constant. (As on object of fixed size moves toward the camera the image increases in size and if it moves away from the camera the image size decreases.) Hence the object was apparently moving in a vertical plane that was perpendicular to the line of sight from the camera. Once cycle of this motion is presented in the figures below to illustrate the nature of the motion.
Observe that the time to complete the oscillation was the difference between 12 sec, frame 9 or 12.3 sec (Figure 16) and 7 sec, frame 17 or 7.43 sec (Figure 8). The difference is 4.87 sec.
In the following figure I have combined several of the previous frames to illustrate the nature of the motion of the UO. All the images except the far right hand image lie on or close to the arc segment of a circle (the white line). (The failure of the rightmost image to lie on the arc might be a result of a slight motion toward the right of the suspension point, IF this were pendulum motion.) Note that the tilt of the UO image also matches quite well the tilt angle of the arc wherever the arc is coincident with the UO image. Notice, in particular, the explanation below the picture of the way the arc was constructed and its implications for how the movie was obtained.
The size scaling described above is proportional. That is, if the width of the picture were 100 ft instead of 10 ft, then the UO width would be 10 ft and the suspension point would be about 140 ft above the tree. This assumes, of course, that the tree was at the same distance as the UO. The height of the image of the tree is about 2 - 3 times the width of the UO, depending upon where one assumes the bottom of the tree image is (not clear in the film). Hence, if the UO were 1 ft wide, and if the tree were at the same distance, then the tree would have been 2 - 3 ft high. If the UO were 10 ft wide then the tree would have been 20 - 30 ft high. [If the tree was not at the distance of the UO then one cannot relate its size to the UO size in this way.] The half angle of the arc (from the lowest point up to the farthest to the right or left) is found from R = 1.35 W and the angle is arctan[(W/2)/1.35W] = arctan[0.37] = 20 degrees.
If the actual distance to the UO were known, then it would be possible to determine its size. There is no obvious distance information in the film. However, there is information in the film which can be used to provide length scaling. This information comes from an unexpected source: Newtonian mechanics combined with time and gravity! This will be discussed below.
It should be obvious to anyone who has played with a yo yo or swung a weight at the end of a string or used a plumb bob or looked at a "grandfather clock," that the motion illustrated in the above figures is at least similar (if not identical!) to that of a pendulum: a weight supported by a cord that is allowed to swing back and forth underneath a fixed suspension point. As stated above, the right-left-right oscillation of the UO began after it moved slowly and steadily to the left and upward in an arc. The center of the arc is above the field of view shown in the video, which was zoomed in on the movie screen. (The center of the arc may have been within the field of view of the camera.) The initial sideways displacement could have been accomplished with an invisible thread attached to the UO. (The same thread could have been used to modify the swinging motion that occurs later in this film segment.) The UO then accelerated downward and to the right following the arc shaped path. The impression one gains from looking at this initial motion is that the UO was released so that it could swing back and forth over the tree. Shortly after the initial right-left-right oscillation there appeared to be some "height adjustment" as the UO moved downward a bit while undergoing a low amplitude left- right oscillation.
The initial UO motion and the motion at other times in the movie is similar to that of a "planar pendulum," a swinging pendulum for which the motion is always within a certain vertical plane (like the Foucault Pendulum). However, at other times the track of the UO was elliptical. At these times the UO moved left and right as before but also toward and away from the camera. Anyone who has played with a weight on a cord knows that the pendulum-like motion can be modified by moving the suspension point (your fingers, if you are holding the cord). By moving the suspension point in a small level circle (circular motion in a horizontal plane) one can make the weight move in a horizontal circle (circular motion in a horizontal plane) instead of only within a vertical plane. When this happens the pendulum is called a "conical pendulum" because the cord sweeps out (or creates in space) a conical surface with the apex at the suspension point.
At times the track of the UO is an ellipse, as it moves toward and away from the camera in between the times when it is at the far left and at the far right. Specifically one sees the following in a typical cycle of motion: the image is at far left and "high"; the image moves downward and to the right and increases in size; the image appears largest when near the tree; the image moves toward the right and upward while shrinking in size; the image reaches a "stopping point" in its rightward motion; the image moves downward and to the left, while shrinking; the image is smallest when at the bottom of the arc near the tree; the image continues to the left while climbing upward and growing in size; the image reaches the maximum leftward motion (and then begins the next cycle). The motion just described is a couterclockwise rotation as seen from above. This motion appears as elliptical on the film, but probably was actually circular. The elliptical appearance would be a result of looking at the circular path from below and at a very small angle to the plane of the circle. Specifically, the vertical height of the elliptical path measured above the tree is about 1/24 of the maximum left-right distance, i.e. the minor axis of the elliptical path on the screen is 1/24 of the major axis. This corresponds to a [arcsin(1/24) = ] 2.4 degree ellipse (the angle between the viewing direction to a circle and the plane containing the circle is 2.4 degrees). Another way of saying this is that the camera was looking upward about 2.4 degrees, assuming that the UO was moving in a horizontal, circular path.
The ratio of the maximum width of the UO image(when highest in the picture) to the minimum width (when lowest in the picture)is about 1.2. Assuming the UO itself did not change size, these image sizes are inversely proportional to the distances of the UO from the camera: the shorter the distance the larger the image, and v.v. If the UO moved in a circular path of radius r, then the distance when closest could be called D and the distance when farthest would be D + 2r and these two distances would be inversely related to the image size ratio: that is, (D + 2r / D) = (image size when closest/image size when farthest) = 1.2. This leads to D = 2r/0.2 = 10 r. If r were 5 ft, then the distance from the camera to closest point of the UO would be about 50 ft. This relationship scales with r, of course.
As pointed out above, the periodic size changes in UO image size are consistent with periodic changes in distance from the camera and, in particular, are consistent with the UO traveling in a horizontal, or nearly horizontal, circle. Furthermore, the thickness (vertical dimension) of the elliptical image of the bottom of the UO itself changes. When the image is largest (i.e., when it is at the highest point over the tree) and therefore closest to the camera, the thickness of the UO image is also largest. The ratio of the image height of the UO ellipse to its width at this point is about 0.35, which corresponds to about a [arcsin 0.35) = ] 20 degree ellipse (a circle viewed from an angle of 20 degrees with respect to the plane that the circle lies in). The look-up angle of the camera was apparently about 2.4 degrees so the actual tilt of the bottom of the UO under these assumptions would have been about 20 - 2.4 = 17.6 degrees. Considering the fact that the UO was probably not moving in a perfect circle and the path probably did not lie within a horizontal plane (because the suspension point was not perfectly rigid or was moved to drive the motion) the near equality between the 17.6 degree tilt of the bottom of the UO and the 20 degree swing angle (cone angle) of the conical pendulum (see above) is very interesting. If the motion were perfectly circular in a horizontal plane these angles would be expected to be equal because the bottom surface would tend to remain perpendicular to the line made by the suspending cord. That is, when the cord hangs straight down the bottom of the UO is horizontal (assuming the center of mass is at the geometric center and directly below the suspension point of the UO). When the cord is moved outward to some angle A (e.g., 20 degrees) with respect to vertical by swinging motion of the UO, the bottom of the UO would be at angle A (e.g., 20 degrees) with respect the horizontal plane (again, assuming perfect symmetry of the UO and assuming the center of mass is directly below the suspension point when suspension is vertical; if the center of mass did not align with the suspension point then the bottom of the UO would not be perpendicular to the suspension).
Never once did the UFO disappear behind the tree, even though its circular motion would have allowed it to do so if the suspension point were above the tree and low enough. During a couple of oscillations the bottom of the UO did appear to be lower than the very top of the tree (it appeared to go behind the very top). As pointed out above, the camera was stationary during this whole film segment.
All of the above discussion has been presented to demonstrate that, to within errors expected because of the rather complex motion of the UO (changing from planar to conical motion and back to planar and changing the amplitude of motion), the geometry of the motion of the UO, i.e., how it appears to move, is consistent with the hypothesis that the UO was moving as would a weight on a suspension if the suspension were moved to "drive" the motion of the weight.
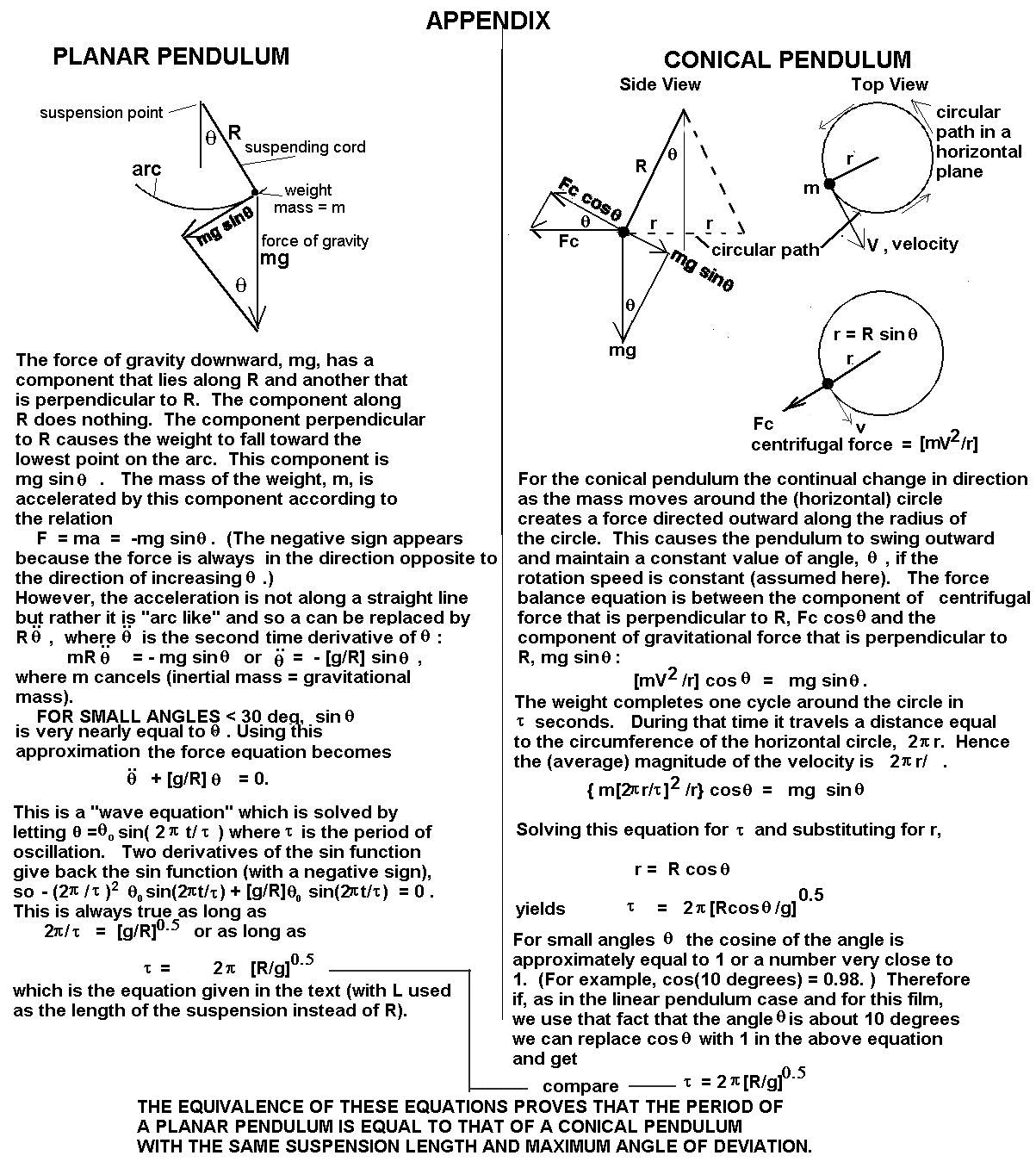
A more sophisticated test of the pendulum hypothesis is based on timing the oscillation periods. For a planar pendulum the period is independent of the weight and depends only upon the length of its suspending cord, as long as the suspension point remains fixed (a fact known to Galileo) and the swing angle is not too great. (If the suspension point moves the period can be modified, usually lengthened.) Hence one could calculate the length of the suspension from the period of the pendulum. As pointed out above, the motion appears to be, alternately, that of a planar pendulum or that of a conical pendulum or a mix of the two.
The relationship between the length and period of the planar pendulum such as one finds in a pendulum clock, is well known. Not as well known is the fact that the period of a conical pendulum (the time to travel around in a horizontal circle) is the the same as that of a planar pendulum of the same length as long as the angular displacement from vertical, i.e., the cone angle, is not too great. In this film the cone half - angle is 20 degrees or less so the period of the conical pendulum is very close to that of the planar pendulum. (The period does change noticeably when the cone angle is much larger than 20 degrees.) The following equation derived in the Appendix can be used to calculate the period of both linear and conical pendulums (when the amplitude of motion is not large) from knowledge of the length of the suspending cord: T = (2pi) times the square root of (L/g). In English units, with L in feet and g, the acceleration of gravity, equal to 32.2 ft/sec^2, the period is in seconds. This equation predicts that, if the length of the suspending cord is constant and the suspension point doesn't move, the period will be constant.
This equation is only correct if no external forces other then gravity are applied to the pendulum and only if the suspension point is fixed in position. The period is changed when forces are applied to the pendulum bob or when the suspension point is moved in order to change its direction and amplitude of swing. The changes of UO motion in the Meier movie would indicate that the suspension was moved because both the direction and amplitude of the UO motion was changed while it was moving. Therefore one would not expect to find the period exactly constant. On the other hand, the near constancy of the period is a prediction of the pendulum hypothesis, a prediction which must be tested.
In order to verify the predicted near constancy of the period I timed a series of the cycles during which the UO seemed to be moving constantly (the motion wasn't decaying or growing much). I found the following values (which include the two values given previous, see above): 4.54, 4.1, 4.3, 4.6, 3.9, 4.2, 4.87, 4.9, and 4.9 sec. During these cycles the motion changed from that of a planar pendulum to that of a conical (or elliptical) pendulum. Clearly the period varied, but not by much. As pointed out above, such variations would occur if the suspension point were moved to change the UO motion from planar to conical. The average period was about 4.5 sec and the standard deviation was about 0.4 sec.
I inverted the above equation to find the length of a pendulum when the period is known: L in feet = g (T/2pi)^2 = 0.81 T^2, with T in seconds. From this equation, if T = 4.5 sec, then L was about 16 ft. When the natural vibration of a pendulum is disturbed by external forces other than gravity (e.g., by pulling on an attached cord, by frictional forces due to the atmosphere or by motion of the suspension point) the period generally increases beyond what one would calculate from the above equations. In other words, since the suspension was moved during this time (to convert from planar to conical motion) the average measured period is probably higher than the value that would be measured if the suspension had been rigid. Thus the minimum measured period may provide a more accurate estimate of the length of the suspending cord. The minimum measured period was 3.9 sec. This value corresponds to a length of about 12 feet. Hence the period data extracted from Meier's film are consistent with a pendulum motion with the length of the pendulum being in the range of 12 - 16 ft.
In the discussion of the geometry of the planar pendulum motion illustrated above (Figure 17), I pointed out that the radius of the arc made by the UO motion is about 1.35 times the width of the arc in the picture. That meant that if the width of the left-right motion was 10 ft, the radius was about 13.5 ft. This value is well within the range of possible values based on the period of the motion. Hence it seems reasonable to conclude from the combined geometric and dynamic (pendulum motion) analysis that the motion of the UO is consistent with it being a small model, say about 1 foot wide, suspended from a point about 14 ft above the lowest point of its swing. The pendulum weight would also have to be attached to a thread or very thin, invisible cord that would allow it to be pulled in various directions to make start the oscillation or to make it change direction. The suspending point could be, for example, a pole that is pushed into the ground or a more complicated structure, that can be moved sideways a small amount order to affect the motion of the UO pendulum.
CONCLUSION
The comparison between the motion of the UO and the motion of a pendulum with a movable suspension point (in order to change the nature of the oscillation from planar to conical and mixtures of the two) has been made. The model hypothesis is that a small UO, perhaps a foot in size, was used along with a several foot high tree that was cut down afterward by Meier or that was a potted tree that Meier moved to the spot and then removed afterward.
Does this mean that I have proven that Mr. Meier's UO was actually a model? Supposedly UFOnauts can co just about anything, including flying a shipin a manner which makes it appear to be oscillating about a fixed, or nearly fixed, suspension point.
So, you be the judge. As for myself, I can't say that Mr. Meier never had a UFO experience. On the other hand, I do not include Mr. Meier's experiences and photos, etc. when I wish to make an argument for the reality of TRue UFOs (TRUFOs).
(NOTE: hearsay testimony barely recalled, but interesting anyway. I was told the following by someone years ago. I was told this by Yaoi or by someone who was aware of Yaoi's investigation. Regarding the tree which, according to Meier, was "removed" by Semjase, if I recall correctly, Yaoi asked the occupant of the farmhouse if he was aware of the tree disappearing. He responded that there had never been a tree at that location.)
LIGHT YEARS by Gary Kinder, Atlantic Monthly Press, New York, 1987 SPACESHIPS OF THE PLEIADES by Kal K. Korff, Prometheus Books, New York, 1995 www.tjresearch.info figu.org
APPENDIX
The period of a pendulum, planar or conical, can be derived from Newton's equation, F = ma, where F is a force applied to an object of mass m to produce acceleration, a. Essentially this says that an accelerating mass reacts against an imposed force. One of the forces acting on the pendulum weight is gravity. The magnitude of that force is mg, where g is the acceleration of gravity at the earth's surface (g varies with radial distance from the center of a gravitating mass). In the planar pendulum the motion is constrained by the suspending cord to move in an arc in a vertical plane. Under this circumstance any force that tries to move the weight along the direction of the suspension has no affect (the suspension prevents the weight from changing its distance from the center of rotation). Forces that are, at any instant, perpendicular to the suspending cord (perpendicular to the radial distance from the center of rotation to the weight) can make the weight move. These are the forces of interest, which determine the oscillation of the pendulum. (The small friction forces which ultimately slow the motion of a freely swinging pendulum are ignored here.)
A conical pendulum also involves forces, and once again, any forces that lie along the instantaneous direction of the suspending cord (radial forces) produce no motion of the pendulum. However forces that are perpendicular to the cord do produce motion. The gravitation force, mg, tries to pull the pendulum downward, while the "centrifugal" force resulting from the circular motion, mv^2/r, tries to make the pendulum move outward. These forces and their applications to the pendulums are presented in the illustration below. The calculations below show that, for small angle oscillations, the period of a conical pendulum of length R is indistinguishably different from the period of a planar pendulum with the same R. These calculations are based on the assumption of a rigid suspension point. If the suspension point is moved small distances the oscillation periods will change slightly. (Large motions of the suspension point can greatly modify or even stop the oscillations.)